Getting queue position from L2 and order book data

In the latest API tutorial added to Databento's docs, we show how you can track the exact queue position of an order with MBO data. This is compared against the estimated queue position from L2 (MBP) data only.

Without MBO data, a common approach to estimate queue position is to define a parametric model for cancellations and update your estimated position each time the aggregate market depth at the price is reduced.

Suppose p(𝑥) denotes the probability of cancel in front of you when your order is positioned 0 ≤ 𝑥 ≤ 1 through the queue, then there are two trivial cases:

• If you just joined the queue, any cancellation or down-modification at the level must come from in front, i.e. 𝑝(𝑥=1) = 1.
• If you are at the front of the queue, 𝑝(𝑥=0) = 0, all cancels and modifies must be from behind.

This becomes a matter of fitting a monotonic function between those two points. Say, a naive model 𝑝(𝑥) = 𝑥 assumes cancels arrive uniformly through the queue. But with some market intuition, you'd expect cancels to be biased towards the back of the queue where orders have poor fill rate and hence lower value.

How strong is this bias? Probably much stronger than you'd think.

In this tutorial, we parameterize this bias -1 < k ≤ 0 where k = 0 (no bias) corresponds to the naive model where cancels are uniformly distributed in the queue, and this bias is stronger as it becomes more negative.

Then, we show a few instances of estimated queue position vs. the exact queue position (ground truth) obtained from MBO data:

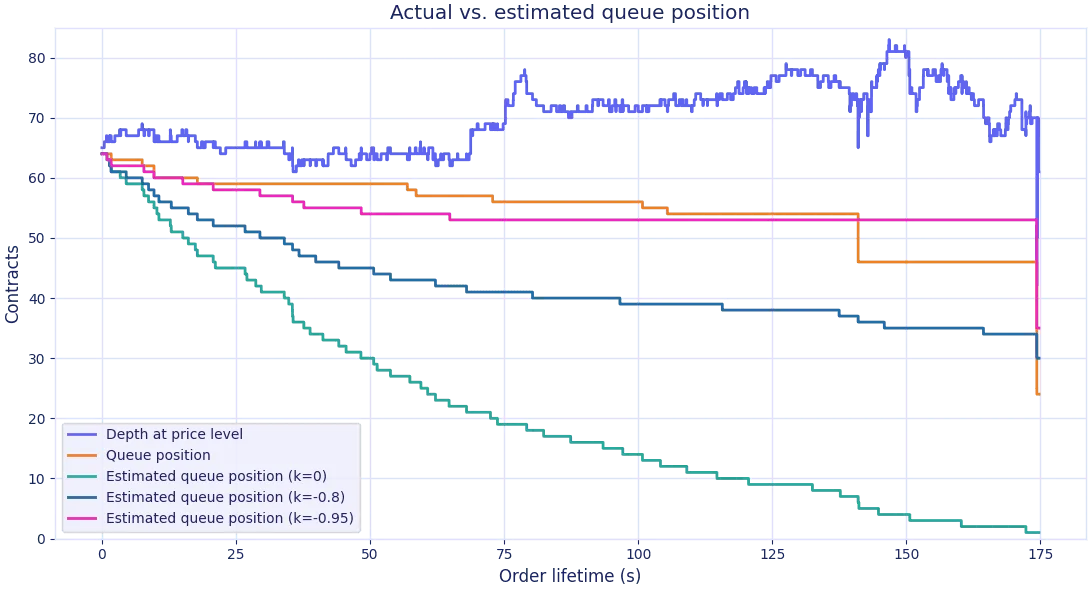
It's evident that cancels are mostly pulled from the back of the queue.

The most common mistake and downside of this approach is underestimating the bias and being overly optimistic your good fill rates: There are many open source and commercial trading platforms that support backtesting with passive orders using L2 data; this feature is sometimes touted as "market replay". All of these platforms we've come across have been overly optimistic. (They also underestimate your adverse fill rates, which is a separate topic.)

Another downside of this approach is that it only works on price levels that are "in scope" given the number of visible levels in your L2 data. For example, if you have MBP-10 data (ten levels of market depth), and if the BBO moves away from your order until it's outside of the top ten levels, then further changes to the price level become censored, making it much harder to estimate your queue position.

Despite these shortcomings, modeling queue position from L2 data is still an important capability since some trading venues don't provide MBO data.